问题描述
给定一个 n个结点(编号 1∼n)构成的二叉树。
进行 m 次询问,每次询问两个结点之间最近的公共祖先是谁或者询问两个结点之间最短路径长度
一 向上标记法 O(n)
从目标结点开始找
-
从目标结点一直向祖先找 所有的祖先都被标记一下
f[x]存的是从i号结点走到 x的最小步数
-
另一个目标结点也同样向上找 遇见第一个被标记的就是他们的最近祖先
g[x]存的是从j号结点走到 x的最小步数
i,j的公告最先为x,那么他们的距离f[x]+g[x]
提示
第2步的g[x]可以不用真正存储用一个k就可以记录当前走了多少步
二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| #include<iostream>
#include<cstring>
using namespace std;
const int N=1005;
int t,n,m;
int f[N],g[N];
int main(){
cin>>t;
while(t--){
cin>>n>>m;
int x,y;
memset(f,0,sizeof f);
for(int i=1;i<=n;i++){
cin>>x>>y;
if(~x)f[x]=i;
if(~y)f[y]=i;
}
while(m--){
cin>>x>>y;
int k=0;
memset(g,-1,sizeof g);
while(x)g[x]=k++,x=f[x];
k=0;
while(y){
if(~g[y]){
printf("%d\n",k+g[y]);
break;
}
k++;
y=f[y];
}
}
}
}
|
从根节点找
-
从根节点一直向某一个结点( i ) 找,对于路径上的每一个结点都进行标记
depth[x]为根节点向i走了x的孩子是谁
-
从根节点向另一个结点( j ) 找,对于路径上的每一个结点都进行标记
depth[x]为根节点到 j的距离
-
从根节点向一个结点找,最后一次公公告结点就是他们最近公共子节点
他们的最短距离depth[i]+depth[j]−2∗depth[x]
提示
第2步和第3步可以同时进行
二叉树的最近公共祖先
二 倍增
特点
可以做到在线出结果 就是输入一对查询 立即返回
状态表示
f[i][j]表示从i开始,向上走2j步能走到的结点。0<=j<=logn
depth[i]表示结点i的深度
- 哨兵:如果从i向上跳2j步会跳过根节点,那么f[i][j]=0
- depth[0]=0
步骤
-
预处理f[i][j] 以及depth[i]
可以递归求 f[i][j]=f[ f[i][j−1] ][j−1]
bfs 可以求depth[i]
-
先将两个点跳到同一层
-
让两个点同时向上跳,一直跳到它们最近公共祖先的下一层
- 而且跳的j要从大到小
- 因为跳的步数比较大 可能会越过最近的公共祖先 而直接遇到了更上面的祖先
- 只要向上跳 二者不一样就说明没有跳到公共的祖先就可以跳 这样可以保证跳到公共祖先下一层
- 假设公共祖先下一层就是f[i][k]那么他们的最近的公共祖先就是f[ f[i][k] ][0]
例题
- 数据范围较小可以直接省略f数组 (也可以直接向上标记)
二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| #include<iostream>
using namespace std;
const int N=1005;
int t,n,m;
int l[N],r[N],p[N];
int depth[N];
void dfs(int k,int u){
depth[k]=u;
if(~l[k])dfs(l[k],u+1);
if(~r[k])dfs(r[k],u+1);
}
int get_lca(int a,int b){
if(depth[a]<depth[b])return get_lca(b,a);
while(depth[a]>depth[b])a=p[a];
while(a!=b)a=p[a],b=p[b];
return a;
}
int main(){
cin>>t;
while(t--){
cin>>n>>m;
int a,b;
for(int i=1;i<=n;i++){
cin>>a>>b;
l[i]=a,r[i]=b;
if(~a)p[a]=i;
if(~b)p[b]=i;
}
dfs(1,0);
while(m--){
cin>>a>>b;
int x=get_lca(a,b);
cout<<depth[a]+depth[b]-2*depth[x]<<endl;
}
}
return 0;
}
|
- 数据范围较大
祖孙询问
- 从跟结点开始预处理f[i][j]以及depth[i]
- 按照上述找到(a,b)的最近公共子结点
- 判断
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| #include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N=4e4+5,M=2*N;
int n,m,root;
int f[N][16],depth[N];
int h[N],e[M],ne[M],idx;
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void bfs(){
memset(depth,0x3f,sizeof depth);
queue<int> q;
q.push(root);
depth[0]=0,depth[root]=1;
while(q.size()){
auto t=q.front();
q.pop();
for(int i=h[t];~i;i=ne[i]){
int j=e[i];
if(depth[j]>depth[t]+1){
depth[j]=depth[t]+1;
q.push(j);
f[j][0]=t;
for(int k=1;k<16;k++)
f[j][k]=f[f[j][k-1]][k-1];
}
}
}
}
int lca(int a,int b){
if(depth[a]<depth[b])swap(a,b);
for(int i=15;i>=0;i--)
if(depth[f[a][i]]>=depth[b])
a=f[a][i];
if(a==b)return a;
for(int i=15;i>=0;i--)
if(f[a][i]!=f[b][i]){
a=f[a][i];
b=f[b][i];
}
return f[a][0];
}
int main(){
cin>>n;
memset(h,-1,sizeof h);
for(int i=0;i<n;i++){
int a,b;
cin>>a>>b;
if(b==-1)root=a;
else add(a,b),add(b,a);
}
bfs();
cin>>m;
while(m--){
int a,b;
cin>>a>>b;
int flag=lca(a,b);
if(a==flag)puts("1");
else if(b==flag)puts("2");
else puts("0");
}
return 0;
}
|
三 Tarjan
特点
Tarjan – 离线求LCA,O(n+m)
在线做法:读一个询问,处理一个,输出一个
离线做法:读完全部询问,再全部处理完,再全部输出
状态表示
在深度优先遍历时,将所有点分成三大类
-
2号点:代表已经访问并结束回溯
-
1号点:代表正在访问
-
0号点:代表还没有访问过
其中所有2号点和正在搜索的1号点路径中已经通过并查集合并成一个集合
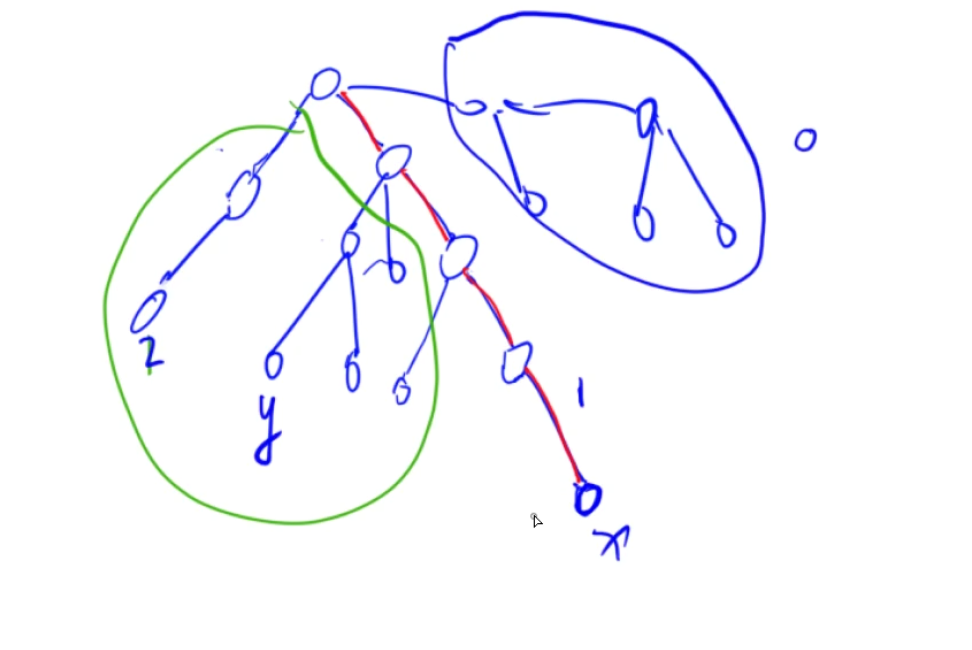
步骤
- 如果当前正在搜索上图中的点x,则找一下所有和这个点x的所有相关的询问,假设询问x和y的最近公共祖先,如果点y在绿色圈中,则可以得到x和y的LCA是图中对应的红色实心点;如果y还没被搜索到,则直接忽略即可,后面的遍历过程中遍历到点y时,就会处理这个询问。
- 因此我们可以使用并查集将所有标记为2的点合并到他们对应的红色实心节点中,当我们需要查看x和某个绿色圈中的点y的LCA时,只需要查看一下点y合并到了哪个点中即可
注意:顺序一定不能乱。
-
当这个点遍历子节点后的时候在把子节点的祖宗更新成当前点
-
只有当前点回溯的时候才可以用这个点来计算所有之前为2的点,因为如果当前点为a,而b是a这条路径的上的点,并且b在a的下面,那么因为b先回溯,所以要等b回溯了之后才能正确的判断a.
-
加入询问的时候要加入两次
query[a].push_back = {b, i}, query[b].push_back(a, i};
-
代码中的trarjan函数中 这两句不能调换顺序
比如在正在遍历的—条路径上a→b→c→d 刚刚遍历完c节点的子树并回溯到c节点那么假如有一个询问是在c−d节点之间对于d节点 st[d]=2
如果先p[j]=u ,那么p[a]=a,p[b]=a,p[c]=b那么在进行anc=find(d)操作时会把d的祖先p[d]直接路径压缩成a节点
如果后p[j]=u,由于p[c]=c那么在进行anc=find(d)操作时p[d]是c节点显然我们要找最近公共祖先,必须先遍历再合并
-
本题没有规定谁是根节点 我们就可以指定一个为跟结点 并不影响
例题
距离
1、先求出所有点到根结点的距离depth[],设x号点和y号点的最近公共祖先是p,则x和y的最近距离等于depth[x]+depth[y]−2∗depth[p]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include<iostream>
#include<cstring>
#include<vector>
using namespace std;
const int N = 10010, M = N * 2;
typedef pair<int,int>PII;
int n,m;
int h[N],e[M],ne[M],w[M],idx;
vector<PII> query[N];
int dist[N],ans[M];
int st[N],f[N];
void add(int a,int b,int c){
w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int k,int father){
for(int i=h[k];~i;i=ne[i]){
int j=e[i];
if(j==father)continue;
dist[j]=dist[k]+w[i];
dfs(j,k);
}
}
int find(int x){
if(x!=f[x])f[x]=find(f[x]);
return f[x];
}
void tarjan(int u){
st[u]=1;
for(int i=h[u];~i;i=ne[i]){
int j=e[i];
if(!st[j]){
tarjan(j);
f[j]=u;
}
}
for(auto q:query[u]){
int a=u,b=q.first,id=q.second;
if(st[b]==2){
int p=find(b);
ans[id]=dist[a]+dist[b]-2*dist[p];
}
}
st[u]=2;
}
int main(){
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
for(int i=1;i<n;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c),add(b,a,c);
}
for(int i=1;i<=m;i++){
int a,b;
scanf("%d%d",&a,&b);
if(a!=b){
query[a].push_back({b,i});
query[b].push_back({a,i});
}
}
for(int i=1;i<=n;i++)f[i]=i;
dfs(1,-1);
tarjan(1);
for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
return 0;
}
|
版权声明: 此文章版权归BrownCutie所有,如有转载,请註明来自原作者



